Blocking out the noise – When should we use outliers in our analysis?

In a previous article, we investigated possible ways to spot anomalies in your data. We shall now follow that up with a discussion about when it makes sense to make use of these data points in your analysis – and when not to do so – as well as looking at some other methods that can be used.   

Outliers – Should They Stay or Should They Go? 

This is arguably the most burning question within this discussion. Identifying these outliers is an excellent first step but deciding whether or not they are crucial to your analyses is a completely different kettle of fish. 

It is best to start by stating that which, to some, may seem obvious. Extreme values should be kept for the following reasons: 

• Visual and statistical tests indicate that they are not anomalies 
• They make up a substantial portion of your data – thus implying they are not outliers 
• The information you are attempting to convey becomes less accurate should they be excluded; an example of this would be when making comparisons between past periods, such as a comparison of the sum or quantity of sales between the previous two years. 

On the other hand, reasons to remove such values include the following: 

• Obvious data entry error or unintentional duplicate 
• The dataset is large enough for this record to have little, if any, impact on your analysis 
• Removal of these values can lead to a truer reflection of your data – the situation mentioned in the introduction might be considered a good example of this. 

There are also other factors that will be involved in your thought process here. In truth, it all boils down to what information you are attempting to convey. If you require insights on your total earnings, your rationale will be very distinct from the thinking process behind getting an overview of what your average client is like. 

If you decide that these extreme values will undermine the accuracy you are attempting to convey, you will likely be swayed towards working without these data points. However, there are some other ways you can tackle this.  

Alternative Approaches and Alliterations 

For convenience, we will assume for now that the target is some alternative for an average value. The easiest alternative that is not impacted by outliers is the median: essentially, this involves your data being sorted in ascending order, and finding the value in the middle. To see this visually, think of the nine circles in the following image as being your data points in ascending order; the blue point, which is in the centre, will be the median. 

Looking back at the example in the introduction, the $1,000,000 sale would not have skewed your insights were you to use the median in place of the average. Nor would it impact your results should you opt for the second option, the trimmed mean. This would once again involve sorting your data in ascending order, though this time, extreme values on either side would be excluded. Taking the following image as a visual example, if the nine circles are your data points, the two red circles would make up the percentage of your data that will be excluded prior to computing the trimmed mean.

If you feel uncomfortable with the idea of reducing the size of your dataset, then another option would be to artificially alter values of extreme data points. Let us once again explain this visually: say that you have 9 data points (represented as circles and sorted in ascending order in the following image), with the red circles representing anomalies that are impacting your analyses.

The light green circle represents the smallest value that is not an outlier, while the dark green one represents the largest such value. A possible solution here would be to replace the outlying values (red circles) by the closest value that is not an outlier. Using these circles as a visual explanation once again, your dataset would now look like this:

As already mentioned, one should tread cautiously when dealing with outliers for analyses for sums, as they may lead to an inaccurate representation of your data. However, suppose you are attempting to forecast the sales you expect to make over an upcoming quarter; would it be fair to include the rare $1,000,000 sale into your thoughts here? Since that was a once-in-a-blue-moon event, it might not be wise to expect it to happen in the near future, so you begin to search for alternative ways to make your predictions.

A relatively uncomplicated way of doing this would be multiplying your chosen measure of location by the number of data points. When you think about it, this is merely a slight twist on the known fact that multiplying your average by the number of data points will give you your existing total.

Once again, we will work with the example mentioned in the introduction, where a single $1,000,000 sale would skew the average, and hence, your forecast. Taking your median or trimmed mean into account instead of your average will ensure you get a more realistic target to aim for. Using that simulated dataset (25 sales with one being at $1,000,000 and the rest under $1000) the difference between the two calculations – in this case, the sum in red versus the median multiplied by the count in yellow – is incredibly stark.

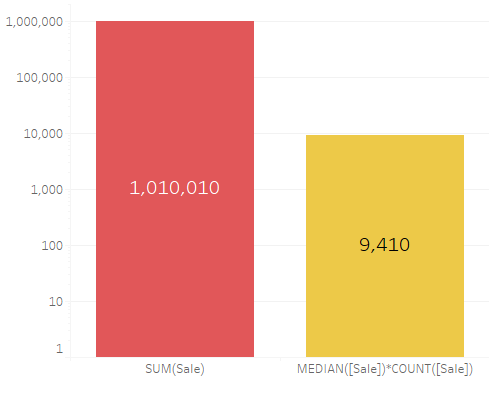
Still operating under the assumption that the gargantuan sale was an event unlikely to be repeated soon, it would be fair to say that the latter value provides a far more realistic indication of what your aims should be.

 

Having reached this point in the article, you may have come to the conclusion that determining whether or not to incorporate your outliers in your analysis – or which alternatives would be most suitable – is something that needs to be decided on a case-by-case basis. If you are interested in finding out more about how to tackle such issues, or other data issues that you may come across, you can reach out to us and request our consultation services with one of our experts at [email protected] – our first consultation is also free of charge.